刚看到这篇文章,把常用的深度学习优化器的intuition解释得非常通俗易懂。特翻译一下当温书啦。
-------------------
2020更新:这篇可以结合另一篇可视化加强理解。
梯度下降的可视化解释(Momentum,AdaGrad,RMSProp,Adam)
-------------------
Understanding Optimizers by Harsha Bommana
在深度学习中,我们有损失的概念,它告诉我们模型在当前时刻的表现如何。现在,我们需要利用这种损失来训练我们的网络,使其性能更好。本质上,我们需要做的就是计算损失并尽量减少损失,因为较低的损失意味着我们的模型将表现得更好。最小化(或最大化)任何数学表达式的过程称为优化,现在我们需要了解如何将这些优化方法用于神经网络。
在神经网络中,每层之间都有许多权重。我们必须了解,网络中的每一个权重都会以某种方式影响网络的输出,因为它们都直接或间接地连接到输出。
因此,可以说,如果我们更改神经网络中的任何特定权重,则网络的输出也将发生变化。
如下图中所示,我们采用了3种不同的方案。在每种情况下,我们都选择一些随机权重,然后对其进行更改。更改选定的权重后,我们还看到了神经网络的哪些部分受到影响,哪些没有受到影响。在所有这三种情况下,网络的最后一层至少有一个受影响的节点。由于最后一层的所有节点也都连接到输出节点,因此可以肯定地说,只要最后一层的某些部分受到影响,输出节点也会受到影响。
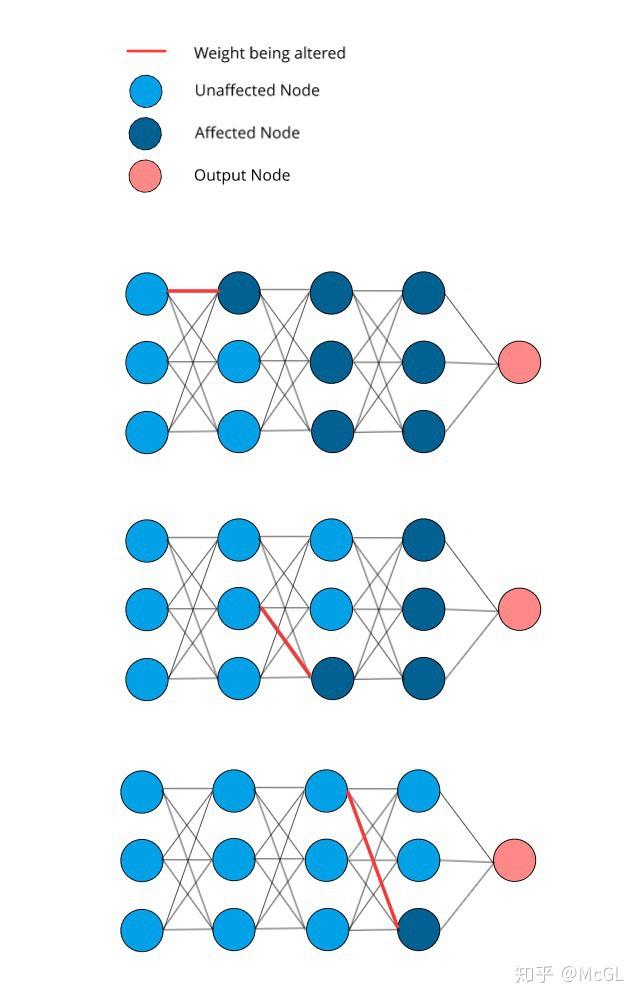
从图中我们还可以观察到,权重距离输出节点较远(更靠近网络的起点),会影响中间的更多节点。因此,可以说它们非常间接地影响输出,因为它们和输出之间有很多权重。靠近输出的权重影响之间的较少节点,因此它们对输出节点有更直接的影响。
现在,我们了解了如何通过更改权重来更改网络的输出,让我们继续了解如何最小化损失函数。改变权重将改变输出。改变输出会改变损失,因为损失是预测值(Y_pred)的函数,该值就是网络的输出。因此,可以说改变权重最终将改变损失。
我们已经建立了权重和最终损失之间的关系,但是到目前为止,我们仅谈论改变。变化可以意味着增加或减少,但我们需要减少损失。因此,现在我们需要了解如何以减少损失的方式更改权重。此过程称为优化。
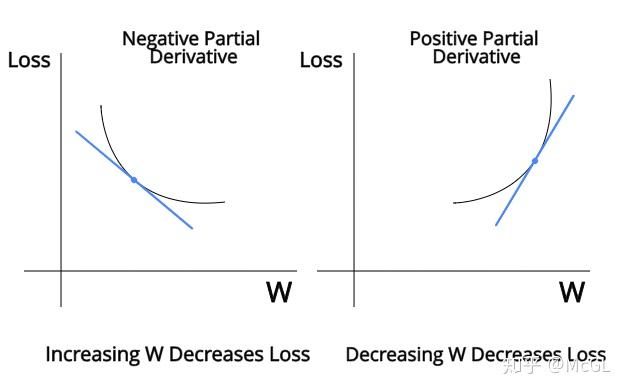
从数学角度来看,我们可以使用偏导数来做到这一点。偏导数使我们能够理解两个数学表达式如何相互影响。让我们看一下X和Y,它们通过某种任意的数学关系相连。如果我们发现X的偏导数相对于 Y, 我们可以了解如何改变X会影响Y. 如果偏导数是正的,这意味着增加X也会对Y.如果是负数这意味着增加X将减少Y.
因此,我们需要找到关于损失的神经网络中每个权重的偏导数。在特定时刻,如果权重的偏导数为正,则我们将减小该权重以减少损失。如果偏导数为负,则我们将增加该权重以减少损失。我们的最终目标是最后减少损失。
此算法称为“ 梯度下降”,也称为“随机梯度下降(SGD)”。这是优化神经网络的最基本方法。这是一个迭代的过程,我们将多次更新每个权重的值直到损失收敛于合适的值。让我们看一下表示单次更新的数学方法:
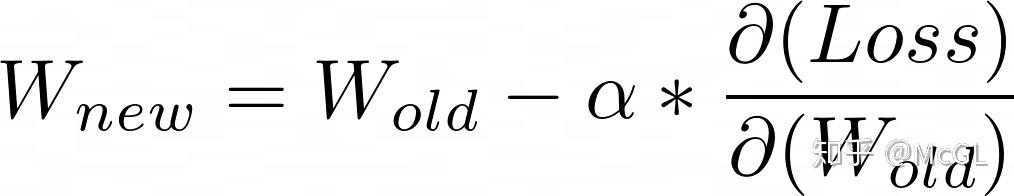
这里的字母符号是学习率。这将影响我们神经网络优化的速度。如果学习率大,则由于较大的步幅,我们将更快地达到损失的极小值,但是同时由于采用了较大的步幅,可能走过头,我们可能无法达到非常好的极小值。较小的学习率将解决此问题,但是要使神经网络的损失减少到一个好的值,需要过多步数。因此,我们需要将学习率保持在最佳值。通常保持alpha=0.01是一个安全值。
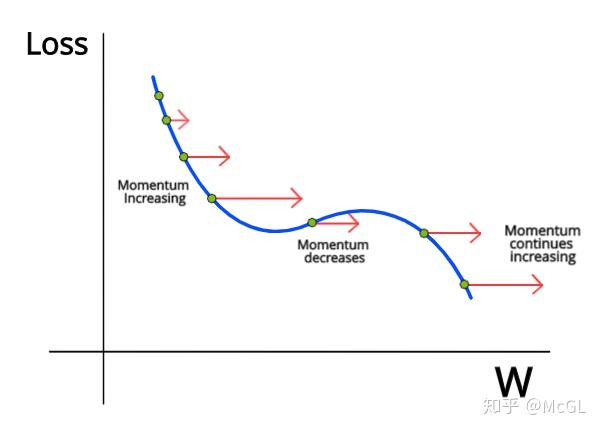
然而,仅梯度下降存在一个大问题。我们并没有将损失推向全局最小值,而只是将其推向了最接近的局部极小值。让我们看看并举例说明。
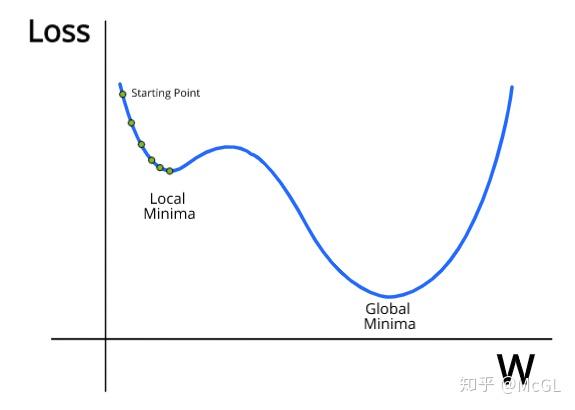
在这里,我们从标记为绿色的点开始。每次更新后,每个随后的绿点代表损失和新的权重。由于局部极小值附近的偏导数(梯度)接近零,因此梯度下降将一直持续到局部极小值为止。因此,它将在达到局部极小值后停留在附近,而不会尝试达到全局最小值。
这是一个相当简单的图,实际上,在存在许多局部极小值的情况下,图要比这复杂得多,因此,如果我们仅使用梯度下降,就不能保证达到良好的损失。我们可以通过动量的概念来解决这个问题。
在动量方法中,基本上我们要做的就是获取权重在执行当前更新之前的更新信息。本质上,如果权重在特定方向上不断移动(增大或减小),它将在该方向上缓慢积累一些“动量”。因此,当它遇到一些阻力不得不向相反方向移动时,由于累积的动量,它仍将继续沿原方向运行一段时间。
这可类比物理学中的实际动量。让我们考虑一个小山谷和一个球。如果我们在山谷的一侧放开球,球将不断滚落,在此过程中,球将朝着该方向发展。最终,当球到达底部时,它并没有在那里停止。相反,它开始在另一侧滚动一段时间,因为它已经获得了一定的动量,即使重力告诉它该下降了。
我们实质上是在尝试通过数学方式重建此场景,以便梯度下降算法绕过局部极小值到达全局最小值。让我们看一下公式:
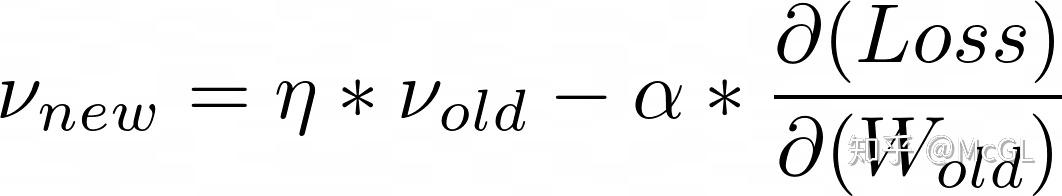
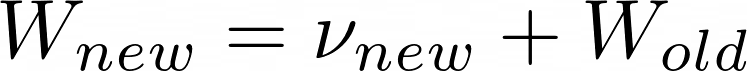
此处,V是动量因子。如你所见,在每次更新中,它实际上将当前导数与先前动量因子的一部分相加。然后我们将其添加到权重中以得到更新的权重。n是动量系数,它决定每次结转多少动量。
由于权重得到更新,动量因子将存储部分以前的梯度。因此,一旦它面对相反的方向的变化(如局部极小值),它将继续沿相同的方向运动,直到动量因子的大小逐渐减小并开始指向相反的方向。大多数情况下,动量因子足以使权重克服局部极小值。
动量的另一个额外优点是,由于梯度的累积,权重会更快的收敛到合适的损失。现在让我们看一下另一种让梯度下降更智能的优化技术。
在NAG中,我们计算近似未来位置梯度代替计算当前位置处的梯度。因为我们要尝试以更智能的方式计算梯度。因为我们使用一个未来的点的梯度,所以动量会在梯度达到最小值之前就开始减小。这样可以提高稳定性,并在收敛时产生较小的震荡,而且,在实践中,其性能优于纯动量。
让我们看看如何精确地使用NAG优化神经网络中的权重。
如果我们看整个动量方程展开:
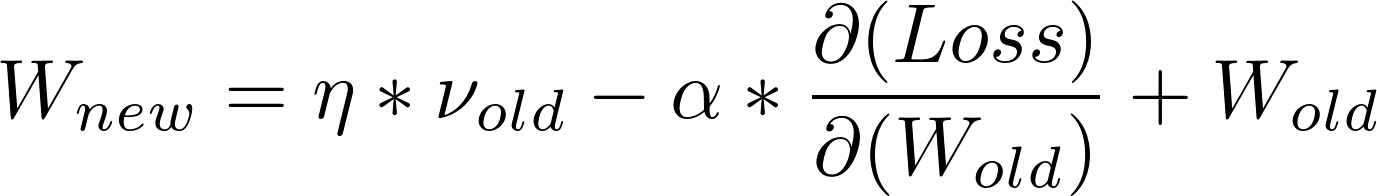
在这里,我们看到下一个W值实质上是将n*v_old与alpha*当前梯度和当前权重相加。考虑到alpha*当前梯度是一个很小的值的事实,我们可以通过将n*v_old与当前W值相加来近似下一个W值。这将给出一个近似的未来W值。
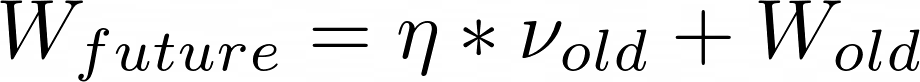
现在,我们要做的不是对当前W值计算梯度,而是对未来W值计算梯度。这样,动量因子就可以在急剧的梯度变化发生之前就开始适应,从而提高了训练时的稳定性。
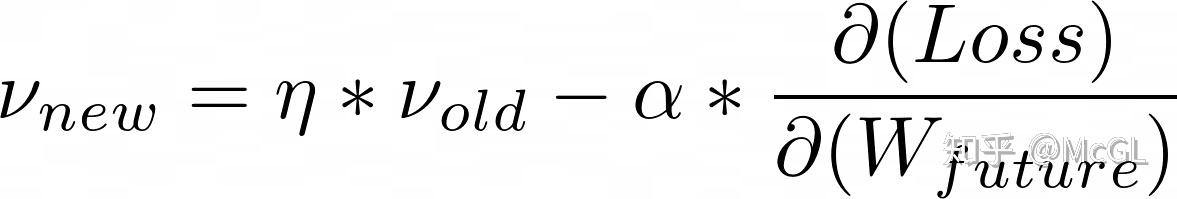
这是NAG的新动量方程。可以看到,我们从W的近似未来值而不是W的当前值获取梯度。
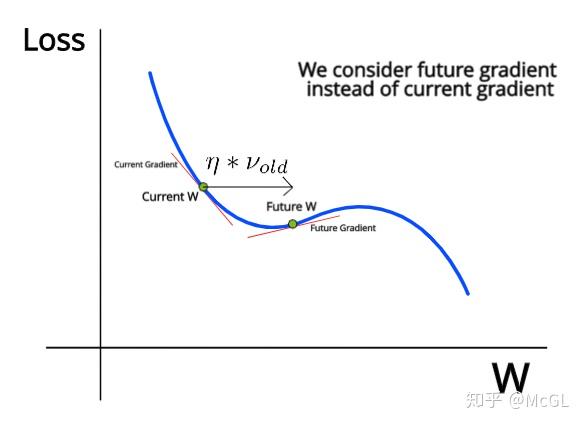
这是一个使用NAG的例子。在当前的W值处,我们添加n*v_old以近似将来的W值。然后,我们计算该点的梯度,并在计算v_new值时使用该梯度代替当前梯度值。如你在本示例中所看到的,即使从技术上讲,在这种情况下动量应该增加,但由于将来的W值具有指向相反方向的梯度,动量反而会在这一点上开始减小。现在让我们看一些自适应优化方法。
在这些方法中,像学习率(alpha)和动量系数(n)这样的参数在整个训练过程中不会保持恒定。相反,这些值将不断适应网络中的每个权重,因此也会随着权重而变化。这些优化算法属于自适应优化范畴。
我们要研究的第一个算法是Adagrad。
Adagrad是自适应梯度的缩写。在这种情况下,我们尝试更改每次更新的学习率(alpha)。在每次更新期间,学习率都会以如下方式变化:如果在短时间内对权重进行过多的更新,学习率将降低;如果对权重没有进行多少更新,则学习率将提高。
首先,每个权重都有自己的缓存值,该值集合了直到当前点为止的梯度的平方。
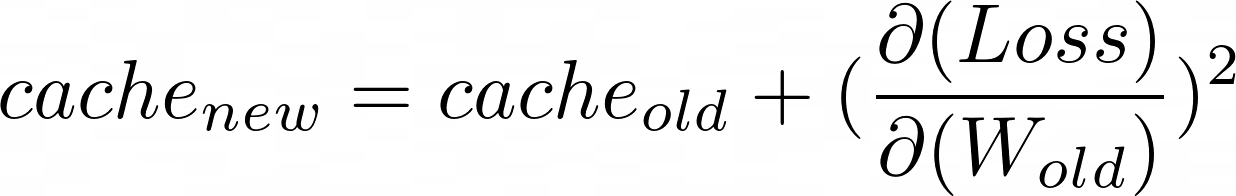
随着训练的进行,缓存的值将继续增加。现在,新的更新公式如下:

这与原始的梯度下降公式具有相同的形式,不同之处在于在整个训练过程中学习率(alpha)不断变化。分母中的E是一个很小的值,以确保不会被零除。
本质上,这里发生的事情是,如果权重进行了非常大的更新,则其缓存值也将增加。其结果是,学习率将变得更小,且权重的更新幅度会随时间而减少。另一方面,如果权重没有进行任何重大更新,则其缓存值将非常小,因此其学习率将提高,从而迫使其进行较大的更新。这是Adagrad优化器的基本原理。
但是,此算法的缺点是,无论权重过去的梯度如何,由于平方不能为负,因此缓存将始终增加一定的量。因此每个权重的学习率最终都会降低到非常低的值以至于训练无法再有效进行。
下一个自适应优化器RMSProp有效地解决了这个问题。
在RMSProp中,唯一的区别在于缓存更新策略。在新公式中,我们引入了一个新参数,衰减率(gamma)。
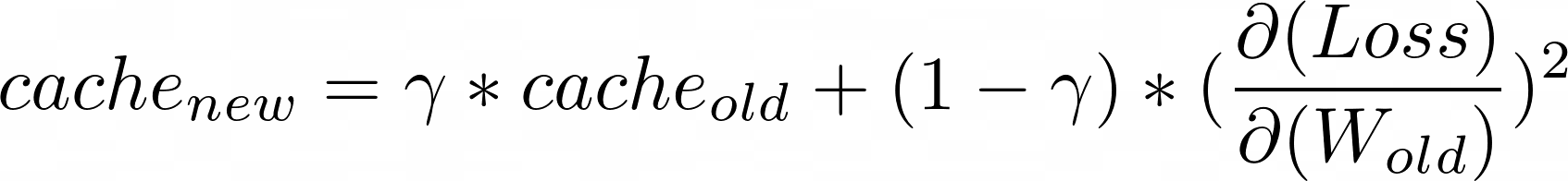
此处的gamma值通常约为0.9或0.99。因此,与adagrad相比,每次更新都会以非常慢的速率添加梯度平方。这样可以确保学习率根据权重的更新方式而不断变化,就像adagrad一样,但是同时学习率不会衰减太快,因此可以继续训练更长的时间。
接下来,我们将研究Adam优化器,它被广泛认为是深度学习优化器通常的最佳选择。
Adam有点像将RMSProp和Momentum相结合。首先,我们计算m值,它将代表当前点的动量。
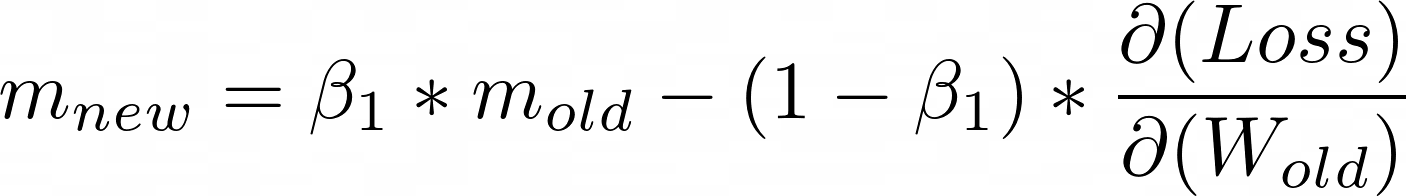
该方程式与动量方程式之间的唯一区别在于,我们将(1-Beta_1)乘以当前梯度,而不是学习率。
接下来,我们将计算累积缓存,它与RMSProp中的缓存完全相同:
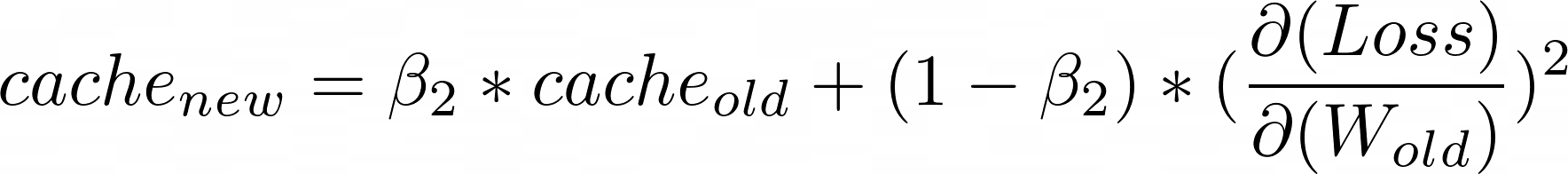
现在我们可以得到最终的更新公式:
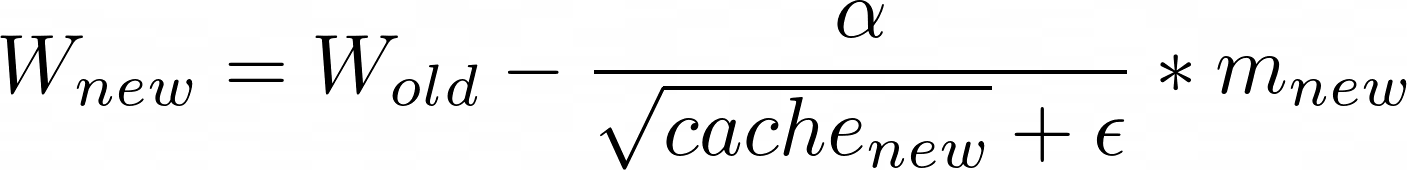
如上,我们通过计算动量来执行梯度的累积,而且我们还通过使用缓存不断地改变学习率。由于这两个特征,Adam通常比任何其他优化器性能更好,并且是训练神经网的首选。在Adam的论文中,建议的参数beta_1为0.9,beta_2为0.99,epsilon为1e-08 .
到此为止,本文涵盖了大多数深度学习从业人员定期使用的大多数重要优化器。希望你学到了一些新知识!谢谢阅读!







